Denoising Example

Suppose we collect complete observations \(y \in \mathbb{R}^N\) of some image \(x \in \mathbb{R}^N\) under a trivial forward model \(\Phi = \mathbb{I}\). Suppose further that our observational instrument introduces some aleoteric uncertainty which can be adequately modelled by a univariate Gaussian \(n = \mathcal{N}(0, \sigma) \in \mathbb{R}^N\). In this case our measurement equation is given by

\[y = x + n.\]

Under these conditions the inverse problem of infering \(x\) given \(y\) is degenerate and thus breaks Hadamards second condition: the solution is not unique and thus the inverse problem is ill-posed. Given that inferences of \(x\) are degenerate it naturally makes more sense to consider the probability distribution of possible solutions; the posterior distribution. Here we use proximal nested sampling (Cai et al 2022), which allows us to sample from this posterior distribution, recovering both an estimate of \(x\) and the plausibility of this estimate. Moreover, as this is a nested sampling algorithm we automatically recover the Bayesian evidence, which naturally allows us to carry out model comparison, through which one can e.g. determine which forward models \(\Phi\) are favoured by the data, or calibrate hyper-parameters of the problem such as \(\sigma\) and regularisation parameters \(\lambda\).

import numpy as np
import ProxNest.utils as utils
import ProxNest.sampling as sampling
import ProxNest.optimisations as optimisations
import ProxNest.operators as operators

Load an image and simulate some observations

# Load Image
dim = 64
ground_truth = np.load('../data/galaxy_image_{}.npy'.format(dim))

# Normalise magnitude
ground_truth -= np.nanmin(ground_truth)
ground_truth /= np.nanmax(ground_truth)
ground_truth[ground_truth<0] = 0

Construct linear operators and mock simulated observations for our stated problem

# A simple identity forward model
phi = operators.sensing_operators.Identity()

# A wavelet dictionary in which we can promote sparsity
psi = operators.wavelet_operators.db_wavelets(["db6"], 2, (dim, dim))

# Define noise parameters
ISNR = 20
sigma = np.sqrt(np.mean(np.abs(ground_truth)**2)) * 10**(-ISNR/20)
n = np.random.normal(0, sigma, ground_truth.shape)

# Simulate mock noisy observations
y = phi.dir_op(ground_truth) + n

Define all necessary parameters and posteior lambda functions

# Parameter dictionary associated with optimisation problem of resampling from the prior subject to the likelihood iso-ball
params = utils.create_parameters_dict(
           y = y,                    # Measurements i.e. data
         Phi = phi,                  # Forward model
     epsilon = 1e-3,                 # Radius of L2-ball of likelihood
       tight = True,                 # Is Phi a tight frame or not?
          nu = 1,                    # Bound on the squared-norm of Phi
         tol = 1e-10,                # Convergence tolerance of algorithm
    max_iter = 200,                  # Maximum number of iterations
     verbose = 0,                    # Verbosity level
           u = 0,                    # Initial vector for the dual problem
         pos = False,                # Positivity flag
     reality = False                 # Reality flag
)

# Options dictionary associated with the overall sampling algorithm
options = utils.create_options_dict(
    samplesL = 1e2,                  # Number of live samples
    samplesD = 1e3,                  # Number of discarded samples
    thinning = 1e1,                  # Thinning factor (to mitigate correlations)
       delta = 1e-8,                 # Discretisation stepsize
        burn = 1e1,                  # Number of burn in samples
       sigma = sigma                 # Noise standard deviation of degraded image
)

# Regularisation parameter
delta = 3e5

# Lambda functions to evaluate cost function
LogLikeliL = lambda sol : - np.linalg.norm(y-phi.dir_op(sol), 'fro')**2/(2*sigma**2)

# Lambda function for L1-norm wavelet prior backprojection steps
proxH = lambda x, T : operators.proximal_operators.l1_projection(x, T, delta, Psi=psi)

# Lambda function for L2-ball likelihood projection during resampling
proxB = lambda x, tau: optimisations.l2_ball_proj.sopt_fast_proj_B2(x, tau, params)

Select a starting position \(X_0\) and execute the sampling method

# Create a 'dirty image' starting position
X0 = np.abs(phi.adj_op(y))

# Perform proximal nested sampling
NS_BayEvi, NS_Trace = sampling.proximal_nested.ProxNestedSampling(X0, LogLikeliL, proxH, proxB, params, options)

ProxNest || Initialise: 100%|██████████| 200/200 [00:00<00:00, 1513.66it/s]
ProxNest || Populate: 100%|██████████| 1008/1008 [00:00<00:00, 2677.04it/s]
ProxNest || Sample: 100%|██████████| 1000/1000 [00:05<00:00, 173.79it/s]
ProxNest || Compute Weights: 100%|██████████| 1000/1000 [00:00<00:00, 1613193.85it/s]
ProxNest || Trapezium Integrate: 100%|██████████| 998/998 [00:00<00:00, 2142228.96it/s]
ProxNest || Estimate Variance: 100%|██████████| 1000/1000 [00:00<00:00, 547344.90it/s]
ProxNest || Compute Posterior Mean: 100%|██████████| 1000/1000 [00:00<00:00, 617263.28it/s]

from skimage.metrics import peak_signal_noise_ratio as psnr
from skimage.metrics import structural_similarity as ssim
from matplotlib import pyplot as plt
plt.style.use('dark_background')
plt.rcParams["font.family"] = "serif"

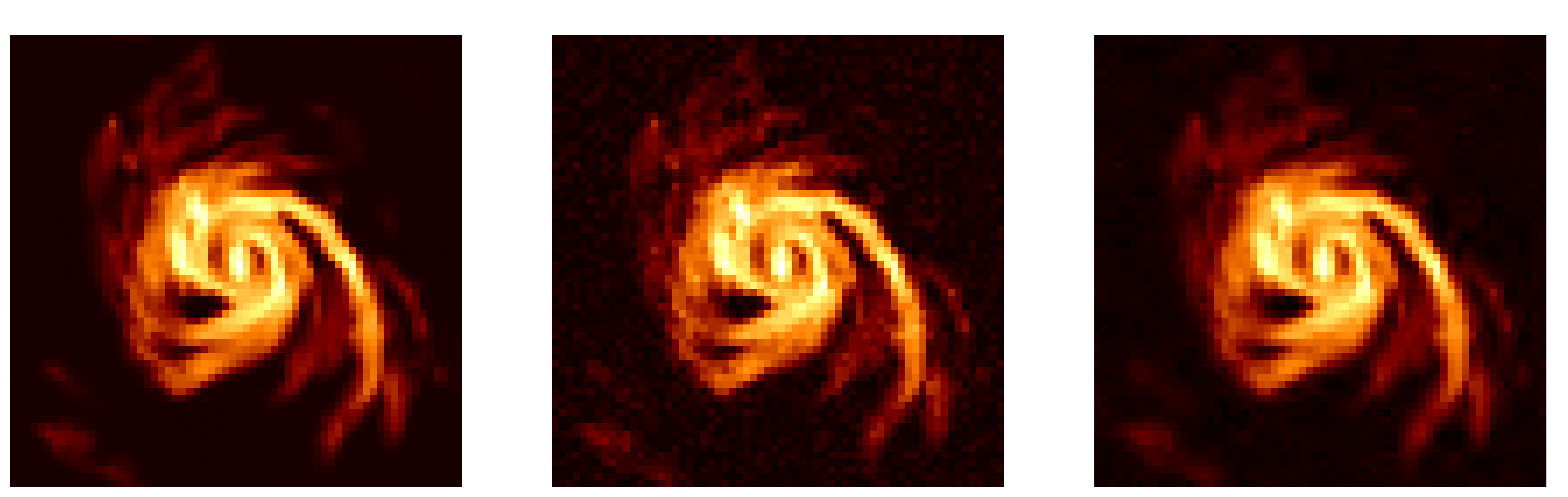
images = [ground_truth, X0, NS_Trace['DiscardPostMean']]
labels = ["Truth", "Dirty", "Posterior mean"]

fig, axs = plt.subplots(1,3, figsize=(20,8), dpi=400)
for i in range(3):
    axs[i].imshow(images[i], cmap='afmhot', vmax=np.nanmax(images), vmin=np.nanmin(images))
    if i > 0:
        stats_str = ' (PSNR: {}, SSIM: {})'.format(
            round(psnr(ground_truth, images[i]), 2),
            round(ssim(ground_truth, images[i]), 2)
            )
        labels[i] += stats_str
    axs[i].set_title(labels[i], fontsize=16)
    axs[i].axis('off')

plt.show()