Differentiable scattering covariances on the sphere#
S2SCAT is a Python package for computing third generation scattering covariances on the sphere (Mousset et al. 2024) using JAX. It leverages autodiff to provide differentiable transforms, which are also deployable on hardware accelerators (e.g. GPUs and TPUs). Scattering covariances are useful both for field-level generative modelling of complex non-Gaussian textures and for statistical compression of high dimensional field-level data, a key step of e.g. simulation based inference.
Important
It is worth highlighting that the input to S2SCAT are spherical harmonic coefficients, which can be generated with whichever software package you prefer, e.g. S2FFT or healpy. Just ensure your harmonic coefficients are indexed using our convention; helper functions for this reindexing can be found in S2FFT.
Tip
At launch S2SCAT provides two core transform modes: on-the-fly, which performs underlying spherical harmonic and Wigner transforms through the Price & McEwen recursion; and precompute, which a priori computes and caches all Wigner elements required. The precompute approach will be faster but can only be run up to \(L \sim 512\), whereas the recursive approach will run up to \(L \sim 2048\), depending on GPU hardware.
Ballpark Numbers [A100 40GB] |
Max resolution |
Forward pass |
Gradient pass |
JIT compilation |
Input params |
Anisotropic (compression) |
Isotropic (compression) |
|---|---|---|---|---|---|---|---|
Precompute |
L=512, N=3 |
~90ms |
~190ms |
~20s |
2,618,880 |
~ 63,000 (97.594%) |
~504 (99.981%) |
On-the-fly |
L=2048, N=3 |
~18s |
~40s |
~5m |
41,932,800 |
~ 123,750 (99.705%) |
~ 990 (99.998%) |
Note that these times are not batched, so in practice may be substantially faster.
Scattering covariances 🧬#
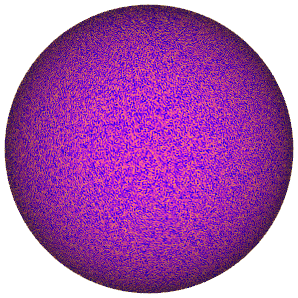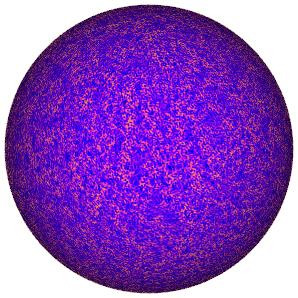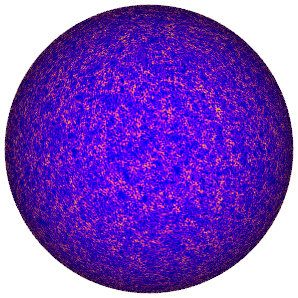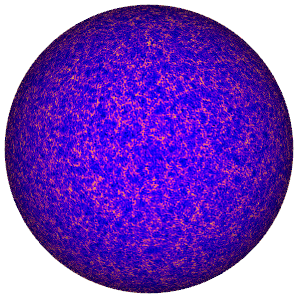
We introduce scattering covariances on the sphere in Mousset et al. 2024, which extend to spherical settings similar scattering transforms introduced for 1D signals by Morel et al. (2023) and for planar 2D signals by Cheng et al. (2023).
The scattering transform is defined by repeated application of directional wavelet transforms followed by a machine learning inspired non-linearity, typically the modulus operator. The wavelet transform \(W^{\lambda}\) within each layer has an associated scale \(j\) and direction $n$, which we group into a single label \(\lambda\). Scattering covariances \(S\) are computed from the coefficients of a two-layer scattering transform and are defined as
where \(W^{\lambda} I\) denotes the wavelet transform of field \(I\) at scale \(j\) and direction \(\gamma\), which we group into a single label \(\lambda=(j,\gamma)\).
This statistical representation characterises the power and sparsity at given scales, as well as covariant features between different wavelet scale and directions; which can adequetly capture complex non-Gaussian structural information, e.g. filamentary structure.
Using the recently released JAX spherical harmonic code S2FFT (Price & McEwen 2023) and spherical wavelet transform code S2WAV (Price et al. 2024) in the S2SCAT code we extends scattering covariances to the sphere, which are necessary for their application to generative modelling of wide-field cosmological fields (Mousset et al. 2024).
Contributors ✨#
Thanks goes to these wonderful people (emoji key):
We encourage contributions from any interested developers.
Attribution 📚#
Should this code be used in any way, we kindly request that the following article is referenced. A BibTeX entry for this reference may look like:
@article{mousset:s2scat,
author = "Louise Mousset et al",
title = "TBD",
journal = "Astronomy & Astrophysics, submitted",
year = "2024",
eprint = "TBD"
}
You might also like to consider citing our related papers on which this code builds:
@article{price:s2fft,
author = "Matthew A. Price and Jason D. McEwen",
title = "Differentiable and accelerated spherical harmonic and {W}igner transforms",
journal = "Journal of Computational Physics",
volume = "510",
pages = "113109",
year = "2024",
doi = {10.1016/j.jcp.2024.113109},
eprint = "arXiv:2311.14670"
}
@article{price:s2wav,
author = "Matthew A. Price and Alicja Polanska and Jessica Whitney and Jason D. McEwen",
title = "Differentiable and accelerated directional wavelet transform on the sphere and ball",
year = "2024",
eprint = "arXiv:2402.01282"
}
License 📝#
We provide this code under an MIT open-source licence with the hope that it will be of use to a wider community.
Copyright 2024 Matthew Price, Louise Mousset, Erwan Allys and Jason McEwen
S2SCAT is free software made available under the MIT License. For
details see the LICENSE file.
